Written by Hassan Almas

Challenges

One of the biggest challenges we face at Valon is modeling mortgages and all the mortgage servicing activities that occur. Today, we have over 50 defined activities, spanning from collecting loan payments to paying taxes through an escrow disbursement. Let’s lay out some of the related challenges we addressed when building our fundamental models:

• Handling the “butterfly effect”: If you’ve watched a sci-fi movie involving time travel, you’ve probably heard of the butterfly effect—someone goes back in time and changes one small thing, but the resulting impact completely changes the present. Well, in mortgage servicing, we have to deal with this all the time. Here’s an example:
  • Imagine a homeowner is charged a late fee for their May mortgage payment. They make subsequent payments, and part of those funds are applied toward paying the late fee. Later, in August, Valon becomes aware that the homeowner was on active deployment with the military, which means they shouldn’t have been charged the late fee in May. We must remove the late fee charge and apply those fees to their principal balance instead. That has cascading effects—now that their principal balance is lowered (as of June), the interest we charged in July and August also needs to be changed! Cascading effects similar to this happen frequently when working with mortgages.
• Allowing teams to work as independently as possible: Our product teams have enough breadth and complexity to cover as is. In the above butterfly effect example, ideally, the team responsible for fees and the team responsible for interest being charged wouldn’t have to coordinate every change, as that would get unwieldy.
• Maintaining the system of record: Given the complexity of cascading changes, it’s essential to keep a clear record of a loan’s state at any point in time—both the state in which it should have been and the state as it was perceived when decisions were made. This is also crucial for auditability by clients and government agencies, as we must be able to justify every action taken with a complete historical understanding of a loan’s evolution.

Modeling a Loan

First, I want to present the conceptual basis we used to address our initial challenges. Enter stage right: loan balances and loan events.

When we began modeling a mortgage, we quickly realized that there are two natural ways to represent it: as a set of events or as a set of balances. Each approach brings unique strengths and tradeoffs.

• The events-based approach (akin to event sourcing) works by breaking the loan into a series of discrete events, such as late fees, loan payments, disbursements, and so on. This method captures everything that has ever occurred on the loan, providing a comprehensive historical record. However, while it excels at showing how we arrived at a particular state, it makes it more difficult and expensive to decide which action should be taken for a new event, since that would require processing the impact of all prior events first to determine the current state.
• The balances-based approach, on the other hand, works by representing a loan as a full set of balances—such as the unpaid principal balance (UPB), last installment date paid, and unpaid fees. This makes it easier to understand the present condition of the loan, like checking whether there’s an outstanding fee balance, without having to process the entire event history. However, this method obscures the historical trail, making it less transparent how we reached the current state.

Upon reviewing the trade-offs, we arrived at a crucial insight: Why not have both?

To take advantage of the strengths of both events-based and balances-based approaches, we capture every change to the loan over time as an event and aggregate the output of each event (a delta to the loan state) into materialized views for ease of use.

To further the idea that events are “decisioning on” the loan state, we built each event to be a computational block, which takes in the materialized loan balances and computes the desired set of changes based on them. This approach helps solve the butterfly effect problem. If something changes on the loan upstream, each event can recompute the resulting state with a domino effect.

To continue the late fee example mentioned earlier, here’s an example showing an initial state where a loan fee was charged and followed by two loan payments. Afterward, a late fee stop event is added, signaling no late fees should be charged—but the effective date of this is before the fee, causing a series of cascading state changes to occur.

• First, the system should no longer apply a fee, so it adjusts the fee balance down to $0.
• Next, the loan payment that had been allocated toward fees should no longer be applied that way, so instead the UPB is reduced by $100.
• Finally, the last payment changes the split between interest and principal because the starting UPB was lower. 

Storing Changing State

It’s a cardinal sin to overwrite information when dealing with financial data, as it makes it impossible to accurately audit the state over time. Although, conceptually, it was easier to think about the cascading state effects as changing data, we needed to make sure there was an immutable and append-only way of representing the data. 

We first decided to store each change as a set of deltas instead of an entire snapshot of the loan state. This allows for significantly less data to be stored than if we were to store the entire balance. (And because, like many startups, we started with the easiest way of doing things, I can say precisely that we were able to reduce the total size of the ledger tables by 95% and the total number of rows used by 97%.) Given that the total number of events that occur over a loan’s lifetime is not too large (~O(1000)), we combine the set of deltas into materialized views of the full loan state when needed.

Once we align on deltas, we need to standardize how to represent the deltas in relation to time. To continue with the sci-fi analogies, because we can go “back in time” to update how something should have occurred, there is no single concept of time that works to represent these changes. A helpful way of approaching this problem is the idea of bi-temporality, in which there are two axes of time on which a change occurs: the date effective (when something happened in a legal sense), and an action date (the date something actually happened, sometimes referred to as a date posted). Both timelines are useful, depending on the type of information needed:

• Date effective timeline: I like to think of this as the official timeline. It represents the state of the loan as things should have happened and is what we reference when calculating new information. Most operations are based on this timeline view. 
  • For example, if we receive an unidentified check on 7/1 and it takes us 2 business days to identify the loan to which the check belongs, we still need to make sure the payment is credited to the homeowner as of 7/1, even if the check wasn’t identified until later.
• Action date timeline: This timeline represents the “real time,” and as such is what reporting and reconciliation are based on. For these kinds of workflows, it is important to represent when we found out about information and actually made the necessary changes. This allows us to say that, “We credited the homeowner as if they had made a payment on 7/1, but we didn’t take this action until 7/2.”

For some examples of how different queries using these dates would work:

• Querying for the UPB with (action date: Now(), date effective: 7/31) is asking what should the UPB have been on 7/31 with the most up-to-date information we have
• Querying for the UPB with (action date:7/31, date effective: 7/31) is asking what the UPB was on 7/31, given the information we had at that point in time

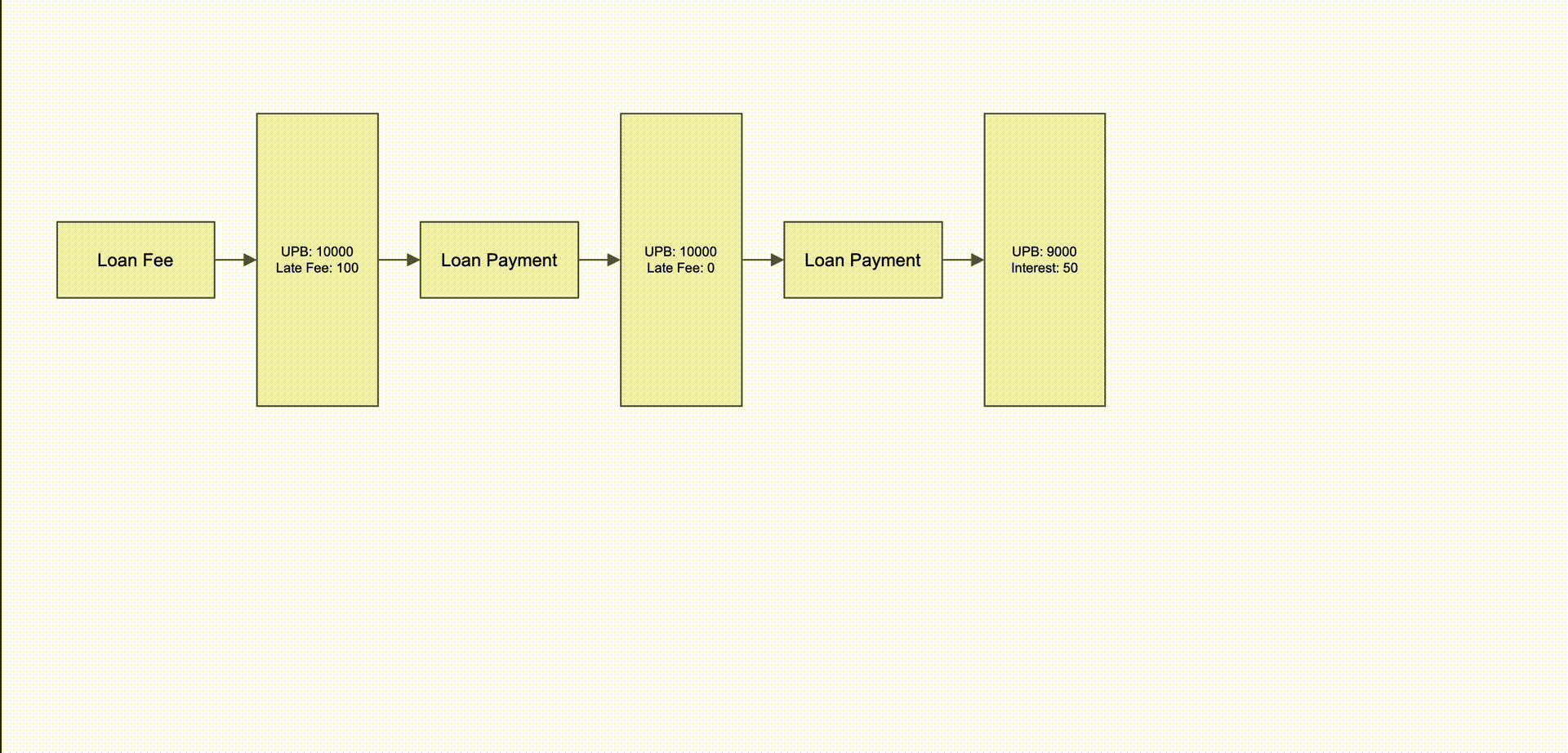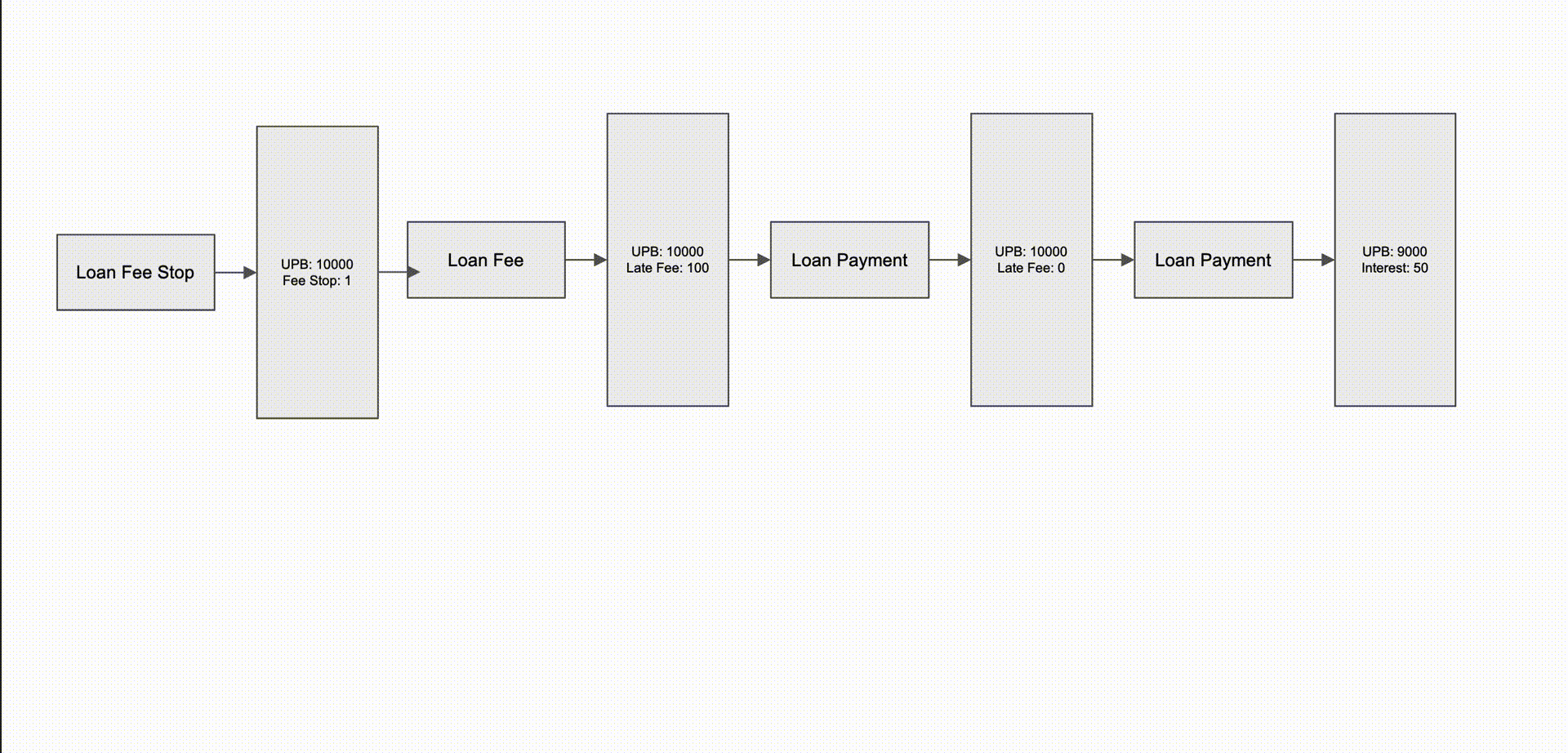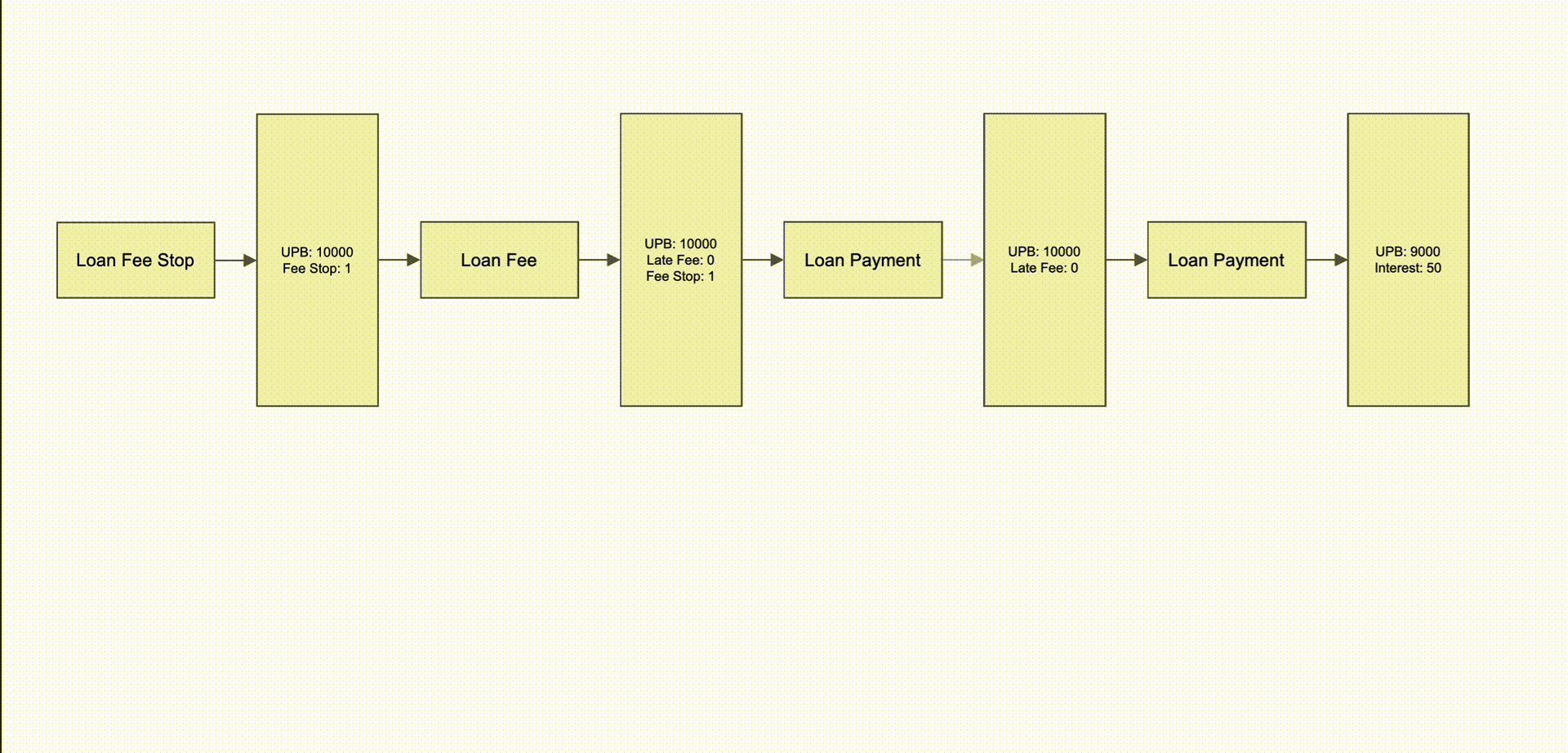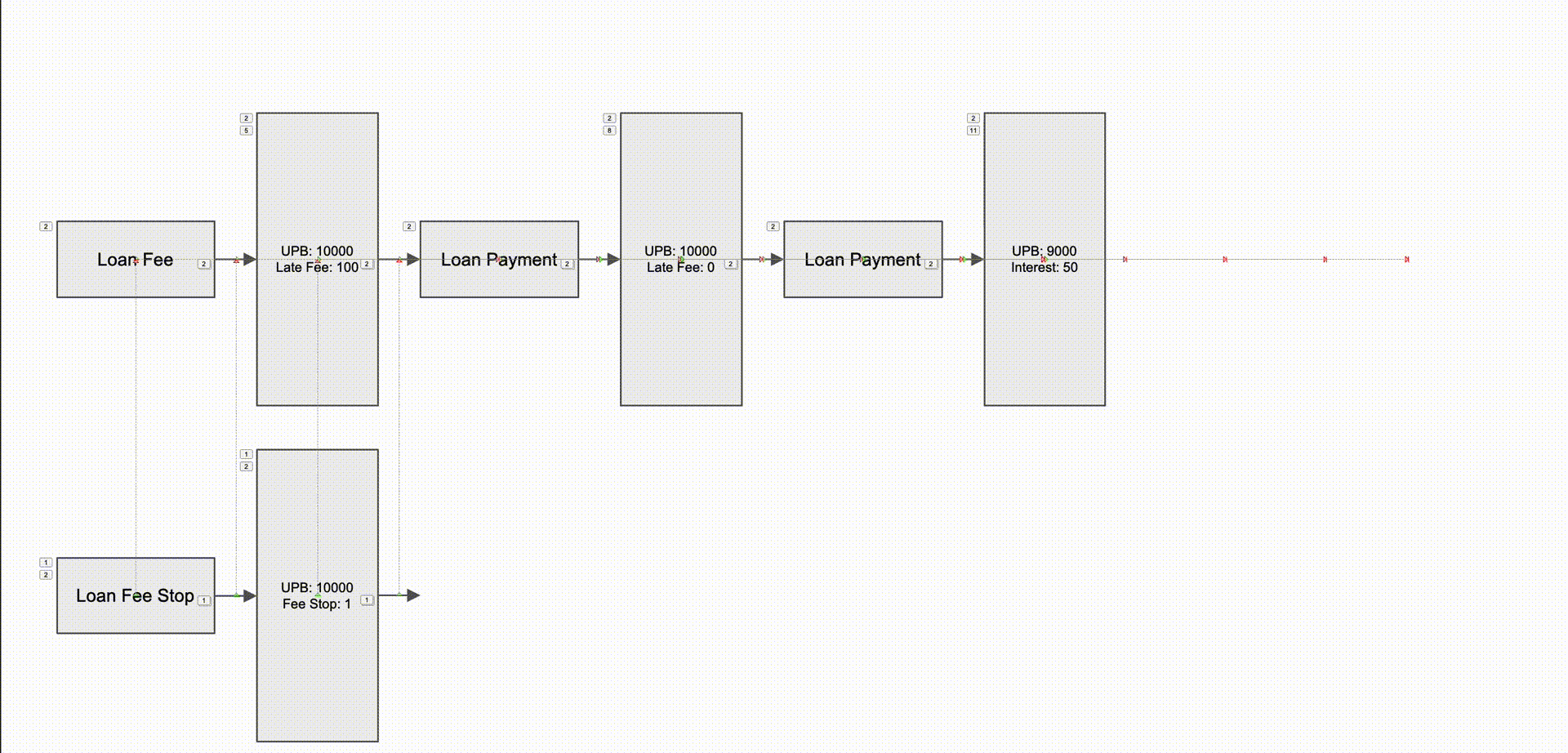
To handle both of these examples, we built a system we call Event Resolutions. The first time an event makes a change, it is stored as a set of deltas—and then any further changes to the event are stored as incremental deltas from the original delta. Each change that occurred because of an event is stored as an event resolution object, with each resolution object being assigned an action date (a monetonically increasing sequence ID to be more specific) that represents the date the change occurred. The set of resolutions is an append-only data store, and any changes are applied as a new delta. Below is a graphical representation of the animation above, but in the event resolutions framework:

Here’s what happened, in words:

• A fee event was created on 7/30, charging a late fee of $100.
• On 8/1, a $100 payment is made, and it is fully allocated to the late fee balance.
• On 8/3, another payment of $1050 is made, reducing the UPB by $1000 and paying $50 in interest.
• On 8/6, Valon is informed that there should be a late fee stop due to the homeowner’s military service status. This late fee stop should be effective as of 7/28, which is the legal date the homeowner should have stopped being charged any fees.
  • This then triggers a series of changes to occur. The changes are effective as of the date of the original event, but the action date is 8/6 (after we learned about the fee stop).
• The fee event no longer should have charged anything, so it adds a new resolution of +$100 to offset the original resolution.
• Now, the first payment also shouldn’t be paying $100 to the late fee, so a new resolution is added, increasing the late fee balance by $100 (netting out to 0 with the original resolution) and reducing the unpaid principal balance by $100.
• Finally, the second payment reallocates, as the amount of interest paid should be lowered (because the UPB was lower), adding a resolution to shift some of the interest paid to further reduce the UPB instead.

Given this storage mechanism under the hood, we then provide client teams with interfaces to fetch the loan’s state projected onto either of the axes. We can collapse the set of resolutions onto the date effective timeline for things like payment accounting, or show it on the action date timeline for reconciliation and external reporting. Collapsing these deltas into snapshots happens behind the scenes for our client teams, allowing them to be concerned only with: “What was the state of this loan at this point in time?” 

Conclusion

Modeling mortgages is inherently complex, and at Valon, we’ve built a system that balances historical accuracy with real-time usability. By embracing both an events-based approach and a balances-based approach, we’ve created a robust loan model that handles cascading state changes while maintaining transparency at every step.

Our use of event sourcing ensures that every action is captured, while modeling the state of the loan as a fixed set of balances provides an easy-to-understand snapshot of the loan’s state at any point in time. By storing all changes as immutable deltas and supporting bi-temporality, we can seamlessly navigate the “butterfly effect” of mortgage servicing, ensuring we can always explain not only what happened but also when and why it happened—maintaining auditability and compliance.

Future Work

The loan ledger is a pure accounting system of record today. I could (and might!) write a whole blog post on the abstractions we have built around money movement, but, in short, each loan gets a virtualized bank account and client teams work with these to make sure funds are moved to and from the relevant places. Once they have moved funds, the teams then have to link those movements to the relevant loan ledger records so that our reconciliation systems can ensure correctness between the two. Right now, we are actively working on building abstractions that allow our client teams to provide one set of instructions to handle both the accounting and cash sides of this problem. If this is something that interests you, feel free to reach out—or stay tuned for future blog posts detailing our progress!

If you’re interested in becoming part of Valon’s team, check out our open career opportunities.